假币问题
本文主要介绍假币问题,分为八币和n币
假币问题
一.实验题目
在八枚外观相同的硬币中,有一枚是假币,并且已知假币与真币重量不同,但不知道假币与真币相比较是轻还是重,可以通过一架天平来任意比较两组硬币,设计一个高效的算法来检测出这枚硬币
二.实验目的
- 深刻理解并掌握减治法的设计思想
- 提高应用减治法设计算法的技能
- 理解这样一个观点:建立正确的模型对于问题的求解是非常重要的
三.实验要求
- 设计减治法实现八币问题
- 设计实验程序,考察用减治技术是否高效
- 扩展算法,使之能处理n枚硬币中一枚假币的问题
四.算法实现分析及结果
八币问题
//确定x1和x2哪个为假币,并且判断重量(n币问题中的cmp也是该函数) void cmp(int x1,int x2,int k) { int ans=max(bi[x1],bi[x2]); if(bi[x1]==bi[k]){ if(ans==bi[x2]) cout<<"假币为第"<<x2<<"个,且较重"<<endl; else cout<<"假币为第"<<x2<<"个,且较轻"<<endl; } else{ if(ans==bi[x1]) cout<<"假币为第"<<x1<<"个,且较重"<<endl; else cout<<"假币为第"<<x1<<"个,且较轻"<<endl; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
+ ```c++
void chaxun()
{
int a=bi[1]+bi[2]+bi[3];
int b=bi[4]+bi[5]+bi[6];
int flag;
if(a==b){
//表明假币一定存在于另外两枚上
cmp(7,8,1);
}
else{
if((bi[1]+bi[4])==(bi[2]+bi[5])){
cmp(3,6,1);return ;
}
if(a>b) flag=1;
else flag=2;
if((bi[1]+bi[4])>(bi[2]+bi[5])){
if(flag==1)
cmp(1,5,2);
else
cmp(2,4,1);
}
else{
if(flag==1)
cmp(2,4,1);
else
cmp(1,5,2);
}
}
}算法分析
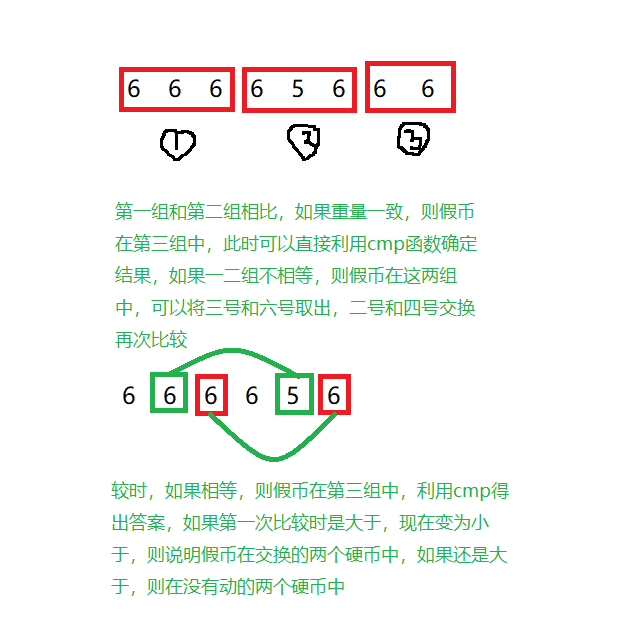
时间复杂度分析
比较次数:这里第二次的交换可以减少比较次数,一次比较即可确定六枚硬币中哪个是假币,前提是得记录第一次比较的情况
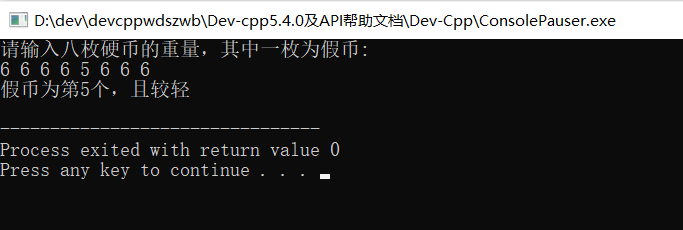
运行结果
n币问题
//计算这一部分的总重量 int getsum(int begin,int last) { int sum=0; for(int i=begin;i<=last;i++){ sum+=bi[i]; } return sum; }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
+ ```c++
//分三段
void chaxun(int first,int last)
{
int n=last-first+1;
//分为三部分
int nn=n/3+n%3/2;
int sum1=getsum(first,first+nn-1);
int sum2=getsum(first+nn,first+2*nn-1);
if(sum1!=sum2){
//假币在当前比较的两部分当中
if(first+2*nn-1-first==1){
cmp(first,first+2*nn-1,last+1);
}
else{
last=first+2*nn-1;
chaxun(first,last);
}
}
else{
//假币在第三堆里
if(n-first-2*nn+1==1){
cmp(last,1,1);
}
else if(n-first-2*nn+1==2){
cmp(last,last-1,1);
}
else{
first=first+2*nn;
chaxun(first,last);
}
}
}算法分析

时间复杂度分析
T(3)=1 n==3
T(n)=T(n/3)+1 n>3
O(n)=$log_3n$
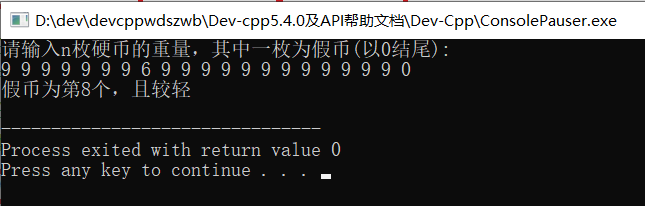
运行结果
五.实验体会
八币问题的核心思想其实是减治,将其划分为三份,每次比较都可以确定一份有假币或者一份无假币,可以优化这一算法的是再第二次比较中除了拿出一组硬币,再交换一组硬币,这样一来可以比较一次确定假币在哪一组,然后拓展到n币问题,也是每次将硬币划分为三组,两组比较,逐步缩减范围,最后得到结果。
减治法和分治法类似,同样是把一个大问题划分为若干子问题,不同的是减治不需要每个子问题都求解,而是选取一组进行求解,可以说是退化版的分治法