本文主要介绍了最近对问题的两种算法，比较时间性能

最近对问题

一.实验题目

设p1=(x1, y1), p2=(x2, y2), …, pn=(xn, yn)是平面上n个点构成的集合S，设计算法找出集合S中距离最近的点对
二.实验目的
- 进一步掌握递归算法的设计思想以及递归程序的调试技术
- 理解这样一个观点：分治与递归经常同时应用在算法设计之中
三.实验要求
- 分别用蛮力法和分治法求解最近对问题
- 分析算法的时间性能，设计实验程序验证分析结论

四.算法实现分析及结果

蛮力法

//与分治法的公共部分
struct point{
    int x,y;
    point(int _x,int _y){
        x=_x;y=_y;
    }
};
double Distance(point a,point b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
} 
1
2
3
4
5
6
7
8
9
10

* ```c++
  //主要部分：双循环挨个遍历计算，取最小值
  for(int i=0;i<N;i++){
  		for(int j=i+1;j<N;j++){
  			if(ans>Distance(p[i],p[j])){
  				ans=Distance(p[i],p[j]);
  			}
  		}
  	}

算法分析
- 算法思想
  
  将每个点与其他点通过遍历求解距离，求出最小值
- 时间复杂度分析
  
  时间消耗在每个点与其他所有点比较，(n-1)+(n-2)+…+(1)–>$\frac{(n-1)*n}{2}$–>O(${n^2}$)
实验结果分析
运行结果

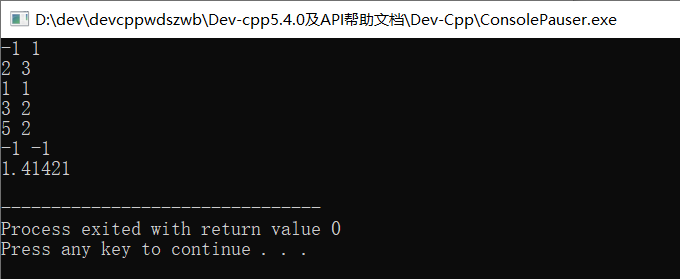
分治法

bool cmp(point a,point b)//按照纵坐标排序
{
    return a.y<b.y;
}
1
2
3
4
5
6

* ```c++
  bool cmp1(point a,point b)//按照横坐标排序
  {
  	return a.x<b.x;
  }

double Closest(point S[],int low,int high)//参数S[]是已经按横坐标排好序的
{
    double d1,d2,d3,d;
    int mid,i,j,index;
    point P[8];
    if(high-low==1) //只有两个点的情况可以直接计算返回
        return Distance(S[low],S[high]);
    if(high-low==2){//只有三个点也可直接计算返回结果
        return min(Distance(S[low],S[low+1]),min(Distance(S[low+1],S[high]),Distance(S[low],S[high])));
    }
    mid=(low+high)/2;
    d1=Closest(S,low,mid);//计算左面部分
    d2=Closest(S,mid+1,high);//计算右面部分
    d=min(d1,d2);
    //cout<<d1<<" "<<d2<<" "<<d<<endl;
    index=0;
    //计算在划分部分左右部分的距离是否比两边的距离小
    for(i=mid;i>=low&&(S[mid].x-S[i].x<d);i--) P[index++]=S[i];
    for(i=mid+1;i<=high&&(S[i].x-S[mid].x<d);i++) P[index++]=S[i];
    sort(P,P+index,cmp);//按纵坐标进行排序
    for(i=0;i<index;i++){
        for(j=i+1;j<index;j++){
            if(P[j].y-P[i].y>=d) break;
            else{
                d3=Distance(P[i],P[j]);
                d=min(d,d3);
            }
        }
    }
    return d;
}

算法分析
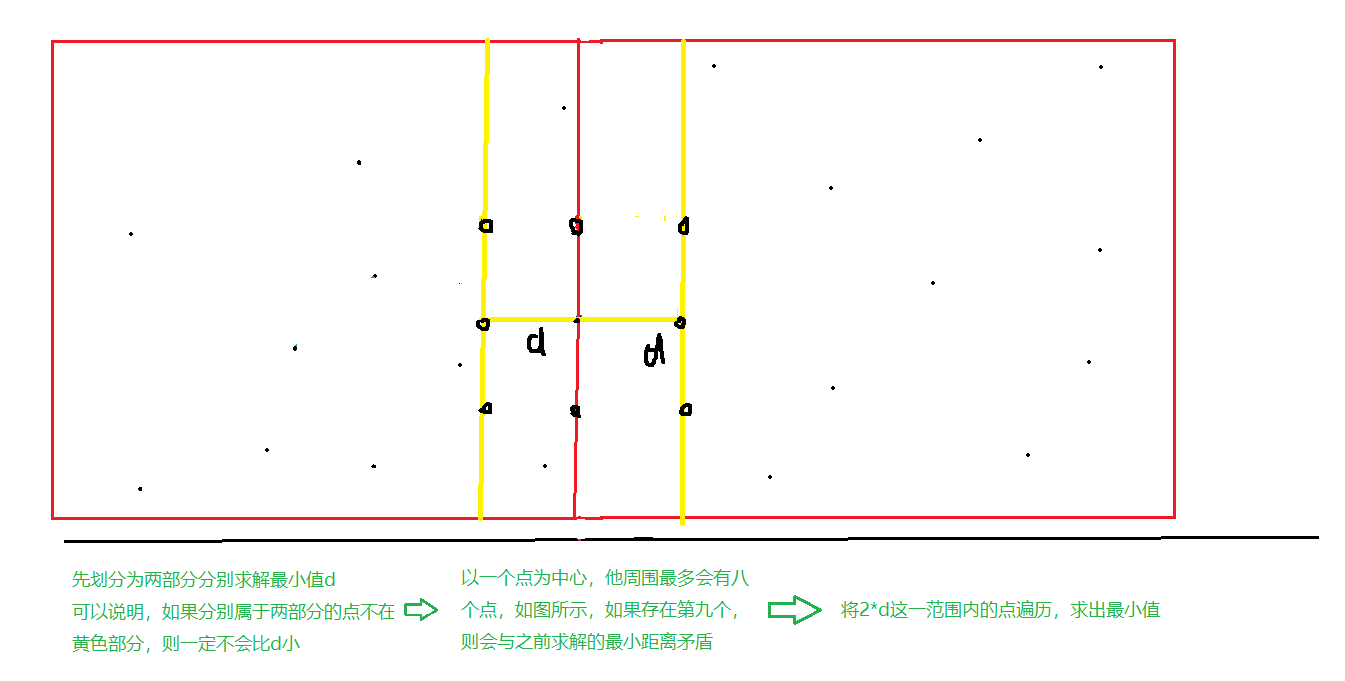
- 算法思想
  
  分治法，划分成两部分，分别计算各部分中的最近对，然后合并子问题，求解分别属于两部分中的点的距离是否会比两部分各自的最近对小
- 时间复杂度
  
  n=2,3时–>O(1)
  
  n>3时–>T(n)=2T(n/2)+n–>O(n*$log_2n$)
运行结果

五.实验体会

通过利用分治法求解最近对问题，熟悉了分治法的三个阶段，划分，求解子问题，合并子问题，划分是将初始问题划分成规模比原来小的同类型问题，求解子问题通常利用递归的方式，再把各个子问题合并起来，算法的效率在很大程度上依赖于合并这一部分。

算法

#算法 #分治