本文是对BM算法的介绍与分析
BM算法
一. 案例分析
目标串:abcdbcbabcbabd
模式串:bcbabc
1>基本思路:从后往前比
abc**==d==**bcbabcbabd
bcb**==a==**bc
a与d不相等
在模式串中找与d相同的字符—-不存在—-模式串直接跳到d的后面
好后缀为bc 找到它的前缀也为bc—-将bc与好后缀对齐
两者移动长度一致
2>abcdbc**==c==**abcbabc
bc**==b==**abc
c与b不相等 在模式串中找与c相同的字符—-下标为1,5—-此时坏字符规则为负数
好后缀为abc,找到前缀为其字串bc,将前缀bc与目标串bc对齐
3>abcdbccabcbabc
bcbabc
!!!匹配成功!!!
二. 代码分析
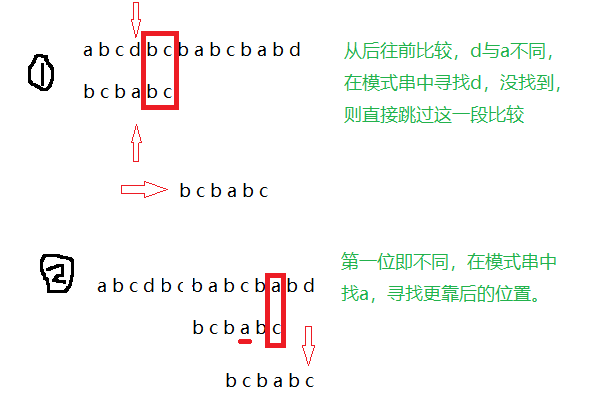
1>坏字符规则:
如果目标串中的字符和模式串的字符不匹配,那么就将目标串中这个字符叫做坏字符。
如果遇到坏字符,可直接判断该字符在模式串中是否存在,如果不存在,则证明前面的部分肯定不会匹配成功,可以直接跳 过,相比于BF算法挨个移动效率有较大提升
如果坏字符在模式串中是存在的,而且可能为多个,为了匹配的精确度,可以取移动少的,即更靠后的相同字符处。
1
2
3
4
5
6
7
8
9
10
|
void badchar(char str[])
{
if(str==NULL) return;
memset(BC,-1,sizeof(BC));
for(int i=0;i<l_str;i++){
BC[str[i]]=i;
}
}
|
2>好后缀规则:
匹配时,遇到坏字符之前的串已经与目标串匹配完毕,叫做好后缀
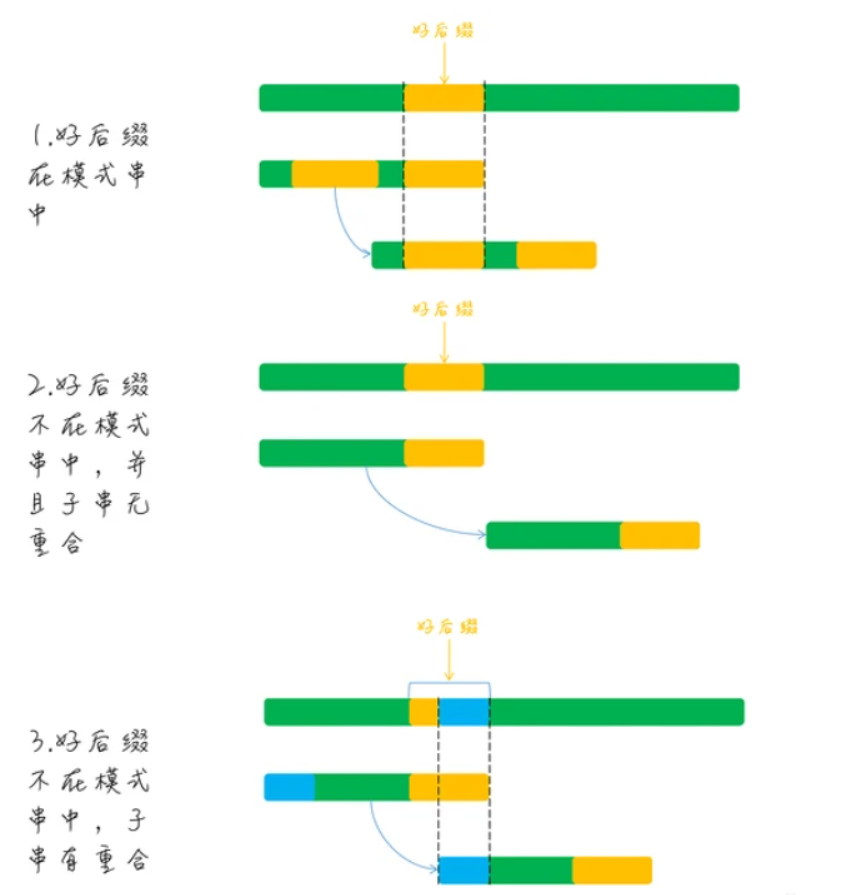
三种情形:
<1>在模式串中没有找到相同的串,直接移动至好后缀之后
<2>找到好后缀的子串,移动至和好后缀子串重合的地方
<3>如果好后缀的子串在模式串存在(与之前不同的是它必须是前缀串),移动至该子串与前缀串重合的地方
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
void suffix(char str[],int suff[],bool prefix[])
{
if(str==NULL) return ;
for(int i=0;i<l_str-1;i++){
int j=i;
int k=0;
while(j>=0&&str[j]==str[l_str-k-1]){
j--;
k++;
suff[k]=j+1;
}
if(j==-1) prefix[k]=true;
}
}
int moveGC(int j,int suff[],bool prefix[])
{
int k=l_str-j-1;
if(suff[k]!=-1){
return j-suff[k]+1;
}
for(int i=k-1;i>=0;i--){
if(prefix[i]){
return l_str-i;
}
}
return l_str;
}
|
3>根据两种不同的移动方案,希望取更大的移动值。
三.完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
| #include<bits/stdc++.h>
using namespace std;
int BC[256];
int l_str,l_ss;
void badchar(char str[])
{
if(str==NULL) return;
memset(BC,-1,sizeof(BC));
for(int i=0;i<l_str;i++){
BC[str[i]]=i;
}
}
void suffix(char str[],int suff[],bool prefix[])
{
if(str==NULL) return ;
for(int i=0;i<l_str-1;i++){
int j=i;
int k=0;
while(j>=0&&str[j]==str[l_str-k-1]){
j--;
k++;
suff[k]=j+1;
}
if(j==-1) prefix[k]=true;
}
}
int moveGC(int j,int suff[],bool prefix[])
{
int k=l_str-j-1;
if(suff[k]!=-1){
return j-suff[k]+1;
}
for(int i=k-1;i>=0;i--){
if(prefix[i]){
return l_str-i;
}
}
return l_str;
}
int BM(char ss[],char str[])
{
if(ss==NULL||str==NULL) return -1;
l_ss=strlen(ss);
l_str=strlen(str);
int suff[l_str];
bool prefix[l_str];
memset(suff,-1,sizeof(suff));
memset(prefix,false,sizeof(prefix));
suffix(str,suff,prefix);
badchar(str);
for(int i=1;i<l_str;i++){
cout<<suff[i]<<" "<<prefix[i]<<endl;
}
int i=l_str-1;
while(i<=l_ss-1){
int j=l_str-1;
while(j>=0&&ss[i]==str[j]){
i--;
if((--j)==-1){
return i+1;
}
}
int moveBC=j-BC[ss[i]];
int moveGS=-10000;
if(j<l_str-1) moveGS=moveGC(j,suff,prefix);
i+=max(moveBC,moveGS);
}
return -1;
}
int main()
{
char ss[]="THIS IS A SIMPLE EXAMPLE";
char str[]="EXAMPLE";
cout<<BM(ss,str);
return 0;
}
|
参考网站

