遗传算法求解TSP问题

本文介绍了基于遗传算法求解TSP问题以及结果的可视化分析

基于遗传算法求解TSP问题

一. 问题描述

​ TSP问题即旅行商问题，属于典型的组合优化问题，理论上来讲，组合优化问题的求解，总是可以用枚举的方式找到结果，例如对于一个简单的对称型TSP问题，可以采用枚举法排列出全部可以选择的路线，然后计算每条线路的长度，根据要求就可以算出总路程的长度，最后比较走不同的路线的长度，找出最短的一条完整路径，这种方法思路简单但是针对于城市数目较少时可以很快算出，但随着城市规模的增大到n，路线就是(n-1)!/2n条，当n较大时就会超出计算机的算力，枚举就没有意义了。

​ 所以现在人们转向寻求有效的启发式算法，这是因为启发式算法使问题在可接受的时间和空间复杂度上去寻找最优解，但无法保证解的有效性和最优性。目前TSP问题的求解算法主要有以禁忌算法，模拟退火算法，遗传算法，蚁群算法等为代表的现代智能优化算法。这些算法虽然思路不同但存在一个共同的目标：求得像旅行商问题等组合优化问题中的难解类问题的全局最优解。

​ TSP问题的数学模型：

​ TSP问题可以定义为，给定n个顶点的无向完全图G = (V,E,r)，要求一个推销员遍历所有城市后回到出发点形成回路C，且使回路C上的权值之和达到最小，其中V是城市点集，E是城市与城市之间的边，r代表权值。

二. 求解问题的方法框架

2.1 遗传算法介绍

​ 遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，它借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法，它能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应的控制搜索过程以求得最优解。遗传算法操作使用适者生存的原则，在潜在的解决方案种群中逐次产生一个近似最优解的方案，在遗传算法的每一代中，根据个体在问题域中的适应度值和从自然遗传学中借鉴来的再造方法进行个体选择，产生一个新的近似解。这个过程导致种群中个体的进化，得到的新个体比原来个体更能适应环境，就像自然界中的改造一样。
​ 遗传算法是计算机科学人工智能领域中用于解决最优化的一种搜索启发式算法，是进化算法的一种。这种启发式通常用来生成有用的解决方案来优化和搜索问题。进化算法最初是借鉴了进化生物学中的一些现象而发展起来的，这些现象包括遗传、突变、自然选择以及杂交等。

2.2 遗传算法基本步骤

流程图：

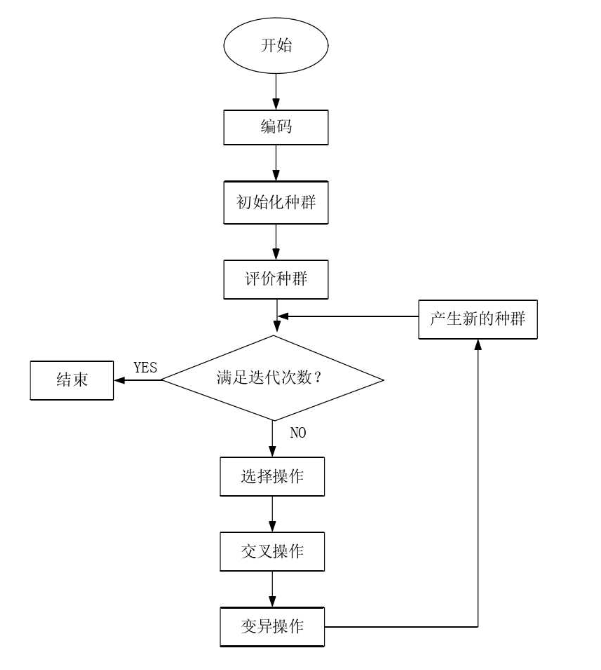
1. 选择编码策略，对所求问题进行编码

   ​ 实现遗传算法的首要目标就是设计对TSP问题的编码方式以及解码方法。因为TSP问题空间的参数不能被遗传算法识别处理，必须根据一定的构造方法将它们转化为由基因组成的遗传空间里的个体，即确定编码方式。

   ​ 本次实验解决C-TSP问题，数据集是中国34个一线城市的最优路线，给出了各个城市的经纬度

   

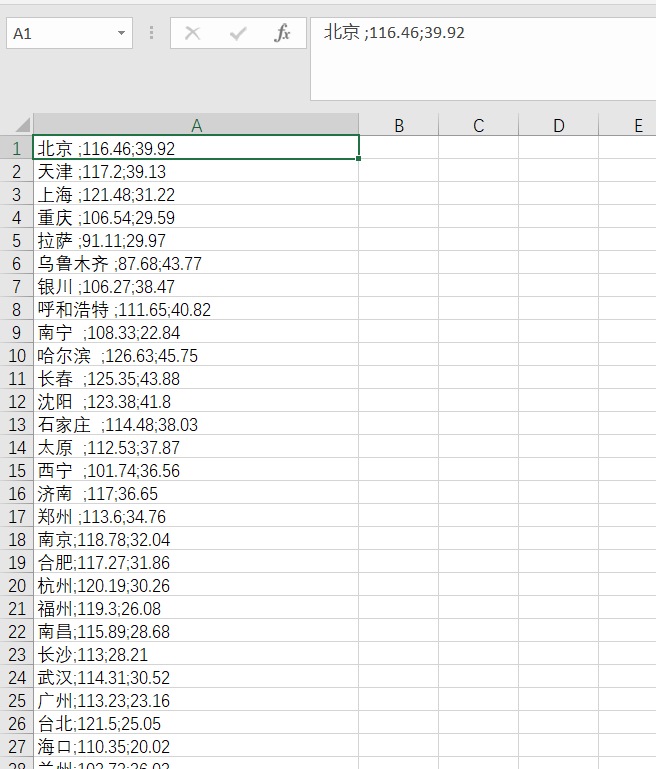
   ​ n个城市的的基因编码方式为：

   ​ 1.给每一个城市一个序号，如1->北京，2->天津，3->上海，……，34->澳门
   2.用包含n个城市的序号的数组序列表示一种路线（个体），数组元素的序号表示旅行的顺序，如{3， 1， 2，……，34}表示的旅行顺序为：上海->北京->天津->……->澳门
   ​ 3.数值序列中值不重复，即每个城市只去一次

2. 初始化种群

   ​ 在选择，交叉，变异等遗传算子选定的情形下,初始种群生成策略的优劣对算法的效率性能和全局收敛性造成很大程度上的影响，通常情况下初始种群的产生是随机性的，根据问题要求，在整个问题空间的范围内设定初始种群规模，起初随机产生一定数量的个体，在挑选优秀的个体进入初始种群中，不断地重复此过程直到取到设定数目的初始种群。利用此方法可以优化程度较低但数量足够的种群。

3. 评估适应度

   ​ 适应度函数是群体中个体生存机会选择的评价指标，其形式直接决定着群体进化行为。在进化搜索的过程中，遗传算法仅参照适应度函数，不需要依靠外部信息搜索种群中每个个体的适应度值进行进化。它直接决定遗传算法的收敛性能以及寻优能力，因此如何设计恰当的适应度函数显得至关重要。通常在遗传算法中，适应度函数是由目标函数转变得到的。依照适应度函数以数字量化处理的方式对实际问题进行优化，达到综合值最小效果的目的。在 TSP问题中，适应度函数通常就以城市序列上的总路径长度的倒数进行定义。

4. 产生新种群

   ​ 产生新种群分为选择，交叉和变异。

   1. 选择

      ​ 这一过程主要是针对具体问题，选择有限的个体参与后期的进化。目的是根据适应度标准对群体进行优胜劣汰的操作，越优秀的个体被选择的概率越高，越容易遗传到下一代种群中，反之适应度较小个体以较低概率进行遗传。

   2. 交叉

      ​ 交叉操作是遗传算法的核心，也是模拟生物进化中关键的步骤，直接决定了遗传算法性能的优劣。交叉算子可以看作基因的相互交流，将两个父代个体的部分基因结构进行替换，重新组合而生成子代新个体的操作。算法的搜索能力通过交叉操作得到极大地提高。

   3. 变异

      ​ 变异算子是根据变异概率将染色体中的基因运用一定方式进行替换形成新的染色体，它模拟生物进化过程中基因发生的突变现象，其基本上决定了遗传算法局部搜索性能的高低。此运算目的是为了增强进化活力，以一定概率更新个体的基因。在遗传算法的中后期，种群中的个体大都逼近最优解，如果只是依赖交叉操作难以产生新的个体。而变异运算可以有效的避免个体同质化，增加个体的多样性，使算法能够较为全面地覆盖问题的解空间。

三. 关键技术

产生新种群是该算法的关键部分

3.1 选择

以下为常见的选择算子：

1. 轮盘赌选择：个体遗传到下一代的概率等于个体适应度值与总体适应度值的比值。
2. 最佳保留选择：首先进行轮盘赌选择操作，然后将父代中适应度最高的个体直接铂贝到子代中。
3. 随机竞争选择：个体进行竞争，选择适应度高的个体遗传到下一代，直到选满为止。
4. 随机联赛选择：每次选择若干个适应度最高的个体复制到下一代种群中。
5. 均匀排序：按照个体适应度高低进行分配每个个体被选中的概率。
6. 排挤选择：新产生的子代替换基因序列相似的父代个体。
7. 精英策略：当前种群中适应度最高的个体不参与遗传操作，替换本代种群中经过遗传操作后适应度最低的个体。

本次实验采用第一种轮盘赌选择(参照书上的数据进行举例)

个体	1	2	3	4	5	6	7	8	9	10
适应度	2.0	1.8	1.6	1.4	1.2	1.0	0.8	0.6	0.4	0.2
选择概率	0.18	0.16	0.15	0.13	0.11	0.09	0.07	0.06	0.03	0.02
累积概率	0.18	0.34	0.49	0.62	0.73	0.82	0.89	0.95	0.98	1.00

当产生一个随机数0.32时 即选择个体2

当产生一个随机数0.42时 即选择个体3

def getOne(self):
    """选择一个个体"""
    r = random.uniform(0, self.bounds)
    for life in self.lives:
        r -= life.score
        if r <= 0:
            return life

        raise Exception("选择错误", self.bounds)

3.2 交叉

1. 顺序交叉

   

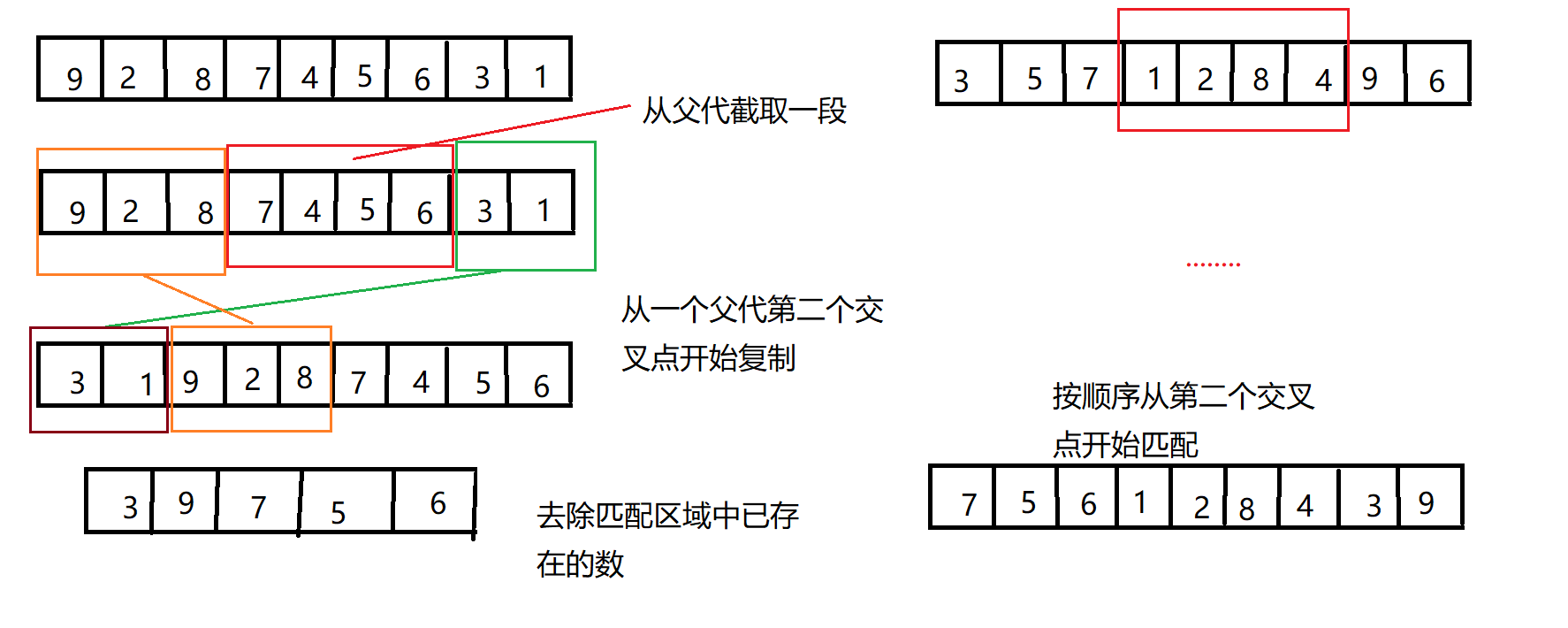
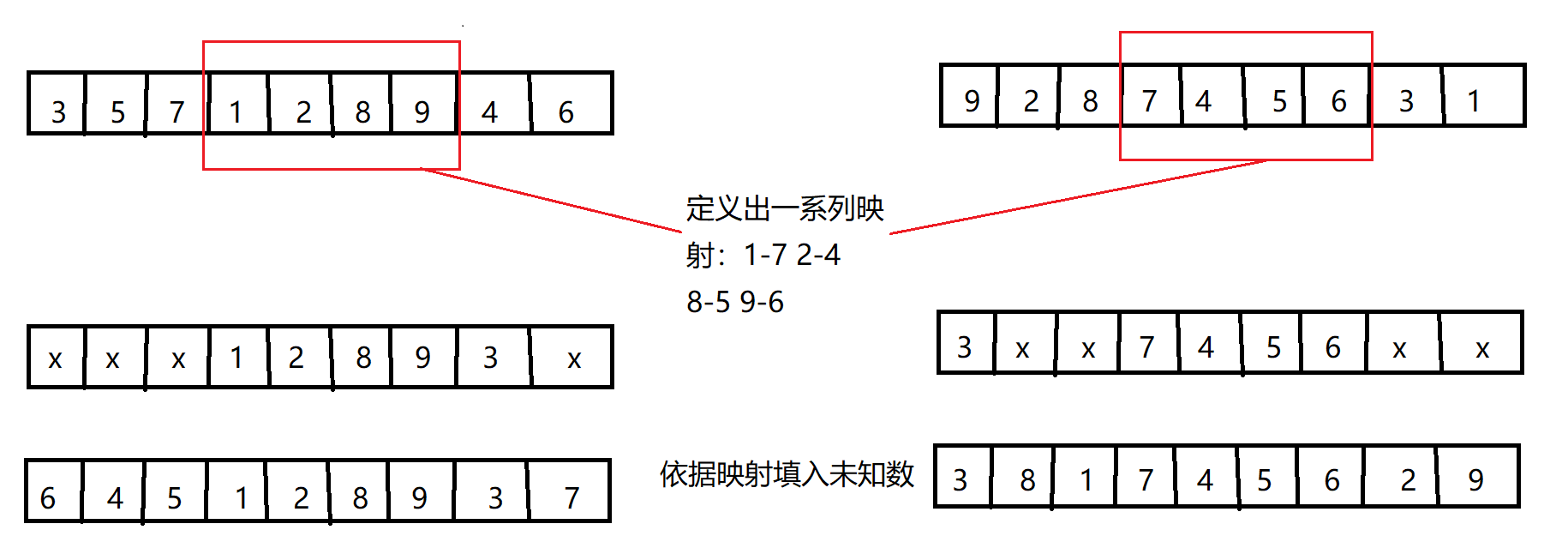
2. 部分匹配交叉

   本次实验采取的方式

   

   def cross(self, parent1, parent2):
       """交叉"""
       index1 = random.randint(0, self.geneLenght - 1)
       index2 = random.randint(index1, self.geneLenght - 1)
       tempGene = parent2.gene[index1:index2]   # 交叉的基因片段
       newGene = []
       p1len = 0
       for g in parent1.gene:
           if p1len == index1:
               newGene.extend(tempGene)     # 插入基因片段
               p1len += 1
               if g not in tempGene:
                   newGene.append(g)
                   p1len += 1
                   self.crossCount += 1
                   return newGene

3. 循环交叉

   

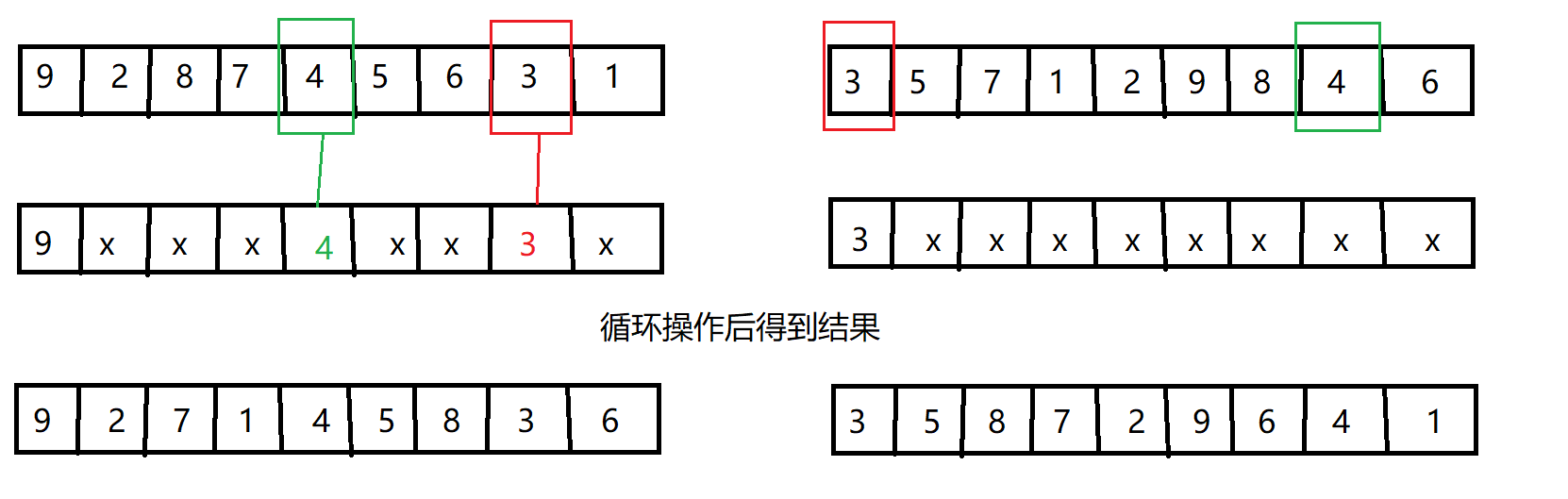
3.3 变异

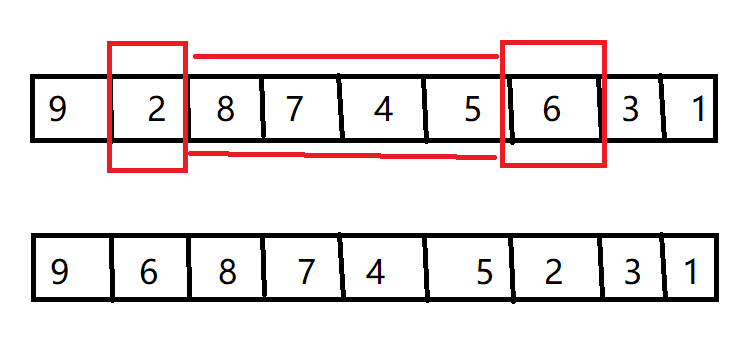
1. 对换变异

   互换元素,本实验采取的变异策略

   

   def  mutation(self, gene):
       """突变"""
       index1 = random.randint(0, self.geneLenght - 1)
       index2 = random.randint(0, self.geneLenght - 1)
   
       newGene = gene[:]       # 产生一个新的基因序列，以免变异的时候影响父种群
       newGene[index1], newGene[index2] = newGene[index2], newGene[index1]
       self.mutationCount += 1
       return newGene

2. 插入变异

   

3. 倒位变异

   将截取点中的进行逆序

   

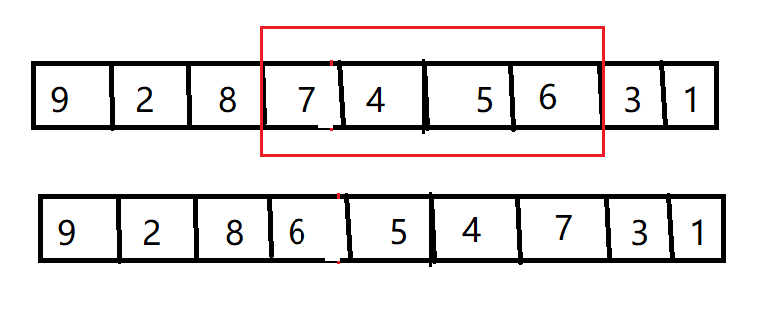
四. 实验结果分析

初始情况

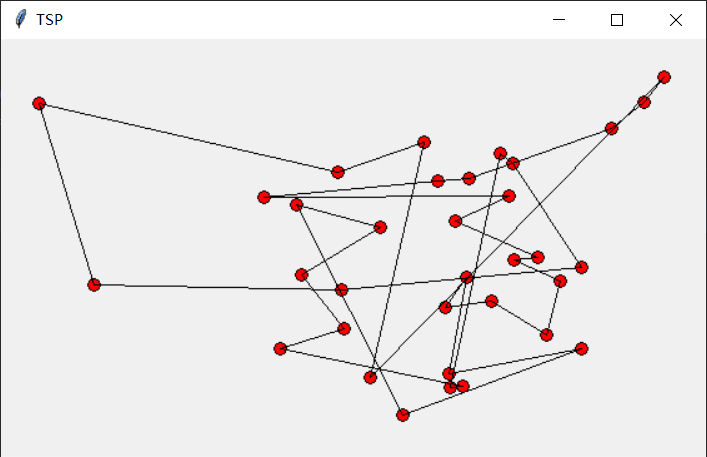
值为：389.702033

迭代514次

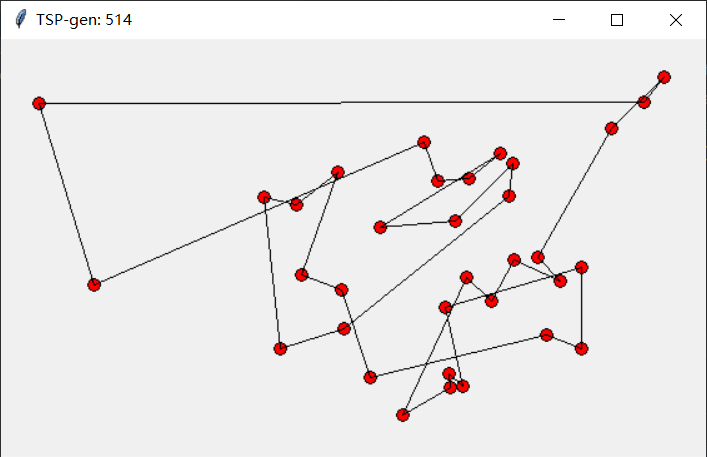
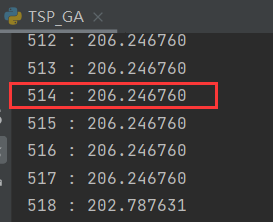
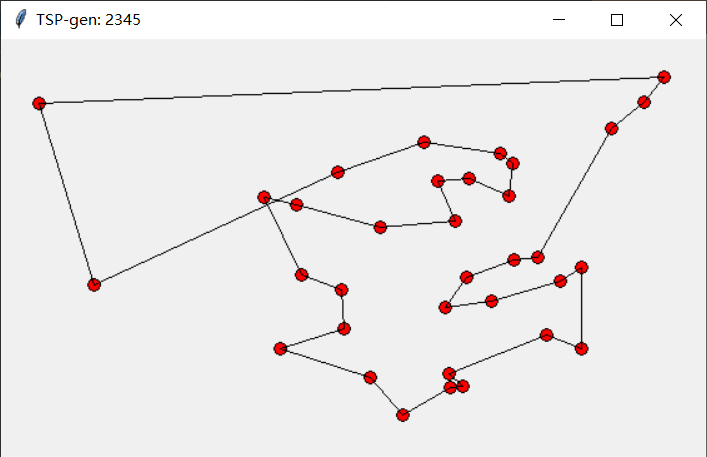
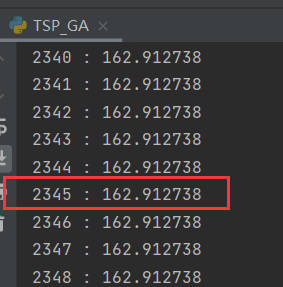
迭代2345次

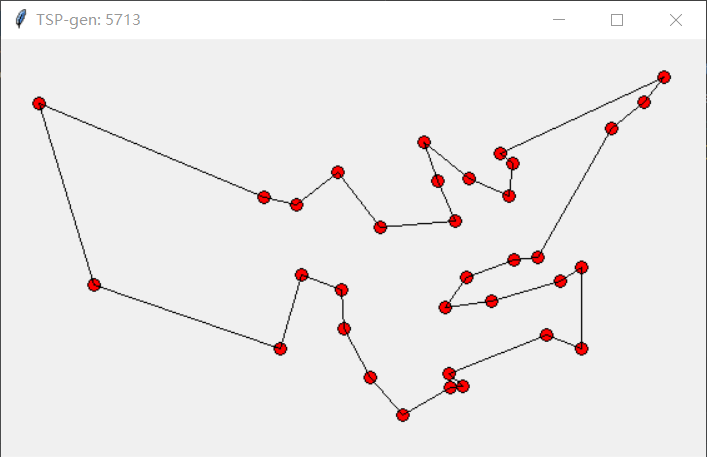
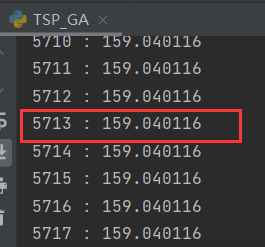
迭代5713次

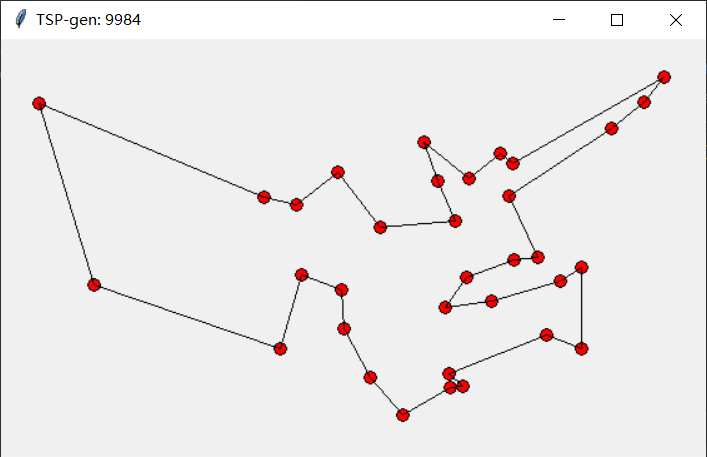
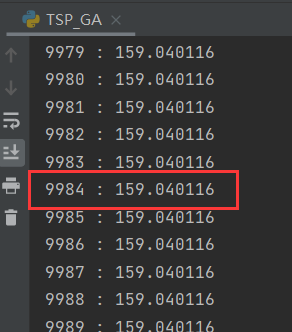
迭代9984次

迭代次数	值
1	389.702033
514	206.246760
2345	162.912738
5713	159.040116
9984	159.040116

对比数据，当迭代次数达到5700次时结果已经趋近最佳

随着迭代次数的增加，对应的值在逐步减小，且从图中也可以看出在向着最优解发展

五. 收获

​ 本次人工智能实验基于遗传算法求解TSP问题收获颇多。虽然之前在算法课上也学过TSP问题，但是只学会了暴力法求解，也就是枚举，经过此实验了解了用遗传算法来进行求解的思路，学习了遗传算法的基本流程，尤其是针对产生新种群的多个方法和他们对应的详细求解过程，并采取其中的一种方法进行处理，对得出的结果进行比对分析。如果还有机会我将对其他产生新种群的方法进行实现并进行对比结果，找出相对更好的方式。