蓝桥杯2022寻找整数

本文是针对2022年蓝桥杯省赛寻找整数的题解

寻找整数

一. 题目

题目链接

二. 题目分析

在求解该题之前需先理解中国剩余定理

​ 在《孙子算经》中有这样一个问题：“今有物不知其数，三三数之剩二（除以3余2），五五数之剩三（除以5余3），七七数之 剩二（除以7余2），问物几何？”这个问题称为“孙子问题”，该问题的一般解法国际上称为“中国剩余定理”。

解法：

• 找出三个数：从3和5的公倍数中找出被7除余1的最小数15，从3和7的公倍数中找出被5除余1 的最小数21，最后从5和7的公倍数中找出除3余1的最小数70。

• 用15乘以2（2为最终结果除以7的余数），用21乘以3（3为最终结果除以5的余数），同理，用70乘以2（2为最终结果除以3的余数），然后把三个乘积相加15∗2+21∗3+70∗2得到和233。

• 用233除以3，5，7三个数的最小公倍数105，得到余数23，即233%105=23。这个余数23就是符合条件的最小数。

解法理解：

有一说一我们的前辈还是很秀的，这解法乍一看还真不知道从何得来！！！

• 首先，将问题拆分成三个小问题

  设n1为取余3等于2的数，n2为取余5等于3的数，n3为取余7等于2的数

  那么现在已知n1取余3为2，如何使n1+n2+n3取余3为2呢？

  这里涉及到一个数学定理：a%b=c —->> (a+k∗b)%b=c

  根据定理可以推断出初步结论

  为使n1+n2+n3的和满足除以3余2，n2和n3必须是3的倍数

  为使n1+n2+n3的和满足除以5余3，n1和n3必须是5的倍数

  为使n1+n2+n3的和满足除以7余2，n1和n2必须是7的倍数

• 上述结论转化如下：

  n1除以3余2，且是5和7的公倍数

  n2除以5余3，且是3和7的公倍数

  n3除以7余2，且是3和5的公倍数

• 求n1的方法：利用逆元求解，当然也可以直接根据定义算，这里方便代码

  35x % 3 == 1 –> 35逆元x为2 –> 70 –> 70*2 =140

• 其余类似

  n2：21x %5 == 1 –> 21逆元x为1 –>21 –> 21*3=63

  n3：30

  转化为代码求解逆元使用费马小定理[一般在mod p是个素数的时候用，比扩展欧几里得快一点而且好写]

  

• n1+n2+n3 = 233 —> 最小为233%(3 * 5 * 7) = 23

一般算法情况：

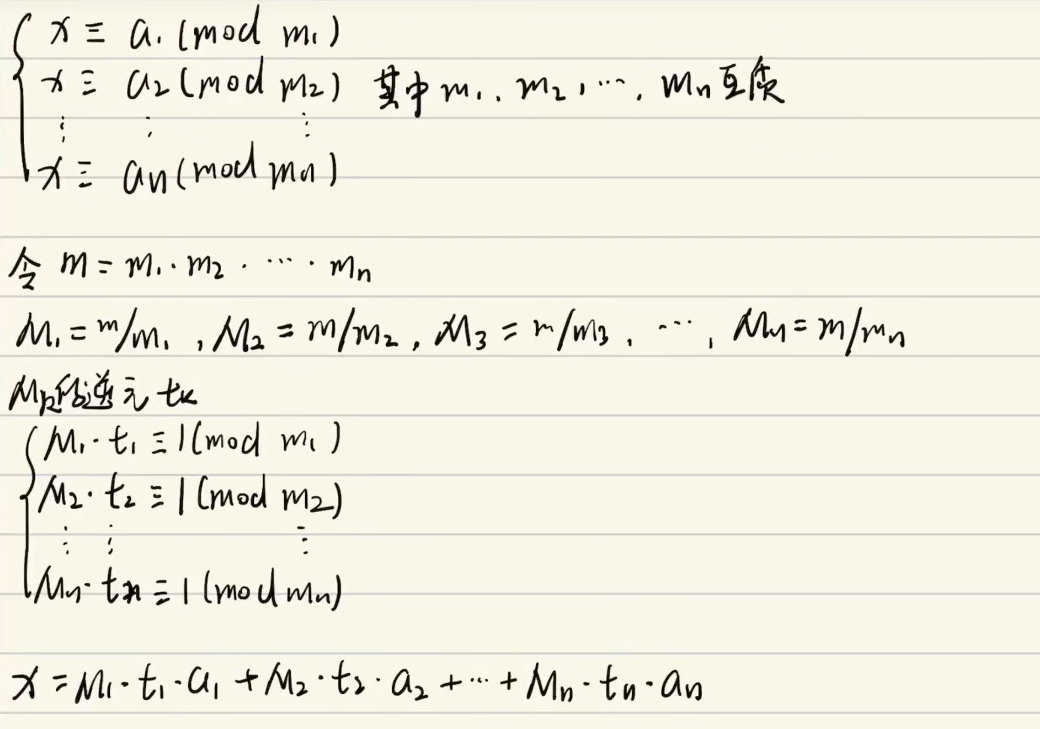
了解完定理之后直接上代码

三. 代码

# 187是11*17
condition = {187: 0, 2: 1, 3: 2, 5: 4, 7: 4, 13: 10, 19: 18, 23: 15, 29: 16, 31: 27, 37: 22, 41: 1, 43: 11,47: 5}  # 所有条件
answer = 0  # 最终答案
remainder = list(condition.values())  # 所有除数
divisor = list(condition.keys())  # 所有余数

m = 1  # 得所有除数的乘积
for i in divisor:
    m *= i

l = len(condition)
# 费马小定理求解逆元
def inv(a, p):
    return a ** (p - 2) % p
for i in range(l):
    Least_Common_Multiple = m // divisor[i]  # 得出剩余数字的最小公倍数
    niyuan = inv(Least_Common_Multiple, divisor[i])
    Least_Common_Multiple *= niyuan
    answer += Least_Common_Multiple * remainder[i]

print(answer % m)

结果：2022040920220409